 |
|
Arjen Dijksman, 2003
Rotating vector models are prevailing techniques when characterizing wave phenomena like simple harmonic oscillator motions, spin representations, circular polarization of particles or pulsar polarization. Considering fundamental particles as rotating vectors have also some interesting consequences, as it confers a characteristic wavefunction to the particle. This wavefunction is derived through analysis of the free rotation of the particle.
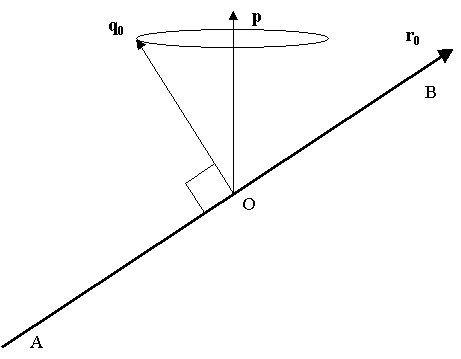
Let AB, a straight-line segment of length r, represent an elementary particle. The vector AB = r unambiguously represents this particle. A and B are symmetric with respect to the geometrical center O. In euclidean 3D space, the kinematic behavior of the AB free particle is described by the combination of:
The latter motion is in fact the resultant of rotations performed simultaneously about several axes. It is similar to the Poinsot motion of a freely rotating body. A Poinsot motion is characterized by the fact that it combines two rotations:
The figure axis is at all times perpendicular to the line segment. For rotating objects without external forces, the figure axis describes a circular cone. The angle between the figure axis and the fixed axis is constant. The rotation speeds wq (about the figure axis) and wp (about the fixed axis) are also constant.
Given the initial parameters, represented in figure 1:
The kinematical specification for r (t) is derived operating two succesive rotations on r0:
This gives:
| r (t) = rq (t) cos wpt + (p x rq(t)) sin wpt + 2 p (p . rq(t)) sin² wpt/2, | (1) |
| with rq (t) = r0 cos wqt + (q0 x r0) sin wqt . | (2) |
The vector wavefunction r(t) fully describes the rotational part of the motion of the line-segment particle. In the case that wp = 0, rq (t) can be expressed in its complex exponential form rq (t) = ||r|| exp (i wqt).
Although the AB-particle has a determined path in 3D euclidean space, the detection process of this particle is non-deterministic. The outcome of a measurement of the position of this particle may be the coordinates of any point of the rotating line-segment. The probability to detect the AB-particle at (x,y,z,t) is therefore directly related to the wave-function r(t) specifying the evolution of this particle. For example, in the case of wp = 0, the probability to detect the particle at x is proportional to the length of the projection of the line segment on the x-axis. This length varies sinusoidally with the frequency 2wq, similarly to the wavefunction amplitude. For a free particle moving in the x direction, the probability wavefunction must be multiplied by a factor exp (ikx), in order to spread out the wave over space. Indeed, nothing tells us where the free particle could show off before it is detected.
The indeterminacy in position can never be smaller than the length r of the particle. Given its instantaneous rotational speed w, assuming that measuring its momentum is done by gauging the recoil effect on another particle or body, the indeterminacy of momentum is proportional to the difference in relative speed of both extremities, i.e. wr. We therefore obtain an indeterminacy relation:
| Dx . Dv = wr2. | (3) |
The rotating vector depicting a fundamental particle is in adequacy with some basic ideas of quantum mechanics, namely that the fundamental particle is characterized by a wavefunction that is related with the probability to find this particle at a definite location at a definite time. It is of interest to express quantum-mechanical wavefunctions in terms of such rotating vectors as it provides a deterministic representation of undetermined detection and interaction processes. A discussion of the use of this rotating vector model has been given in a preceding article 1, namely for the modeling of Young’s double slit experiment and for the interpretation of the difference between massless and inertial particles.
 |
|