The Concept Of Inertia
Arjen Dijksman, 2003
There are at least two ways to restore
determinism in the probability wavefunction of a particle:
- Having point-like or small spherical
singularities guided by a wave, like Bohmian or De
Broglie pilot-wave and double solution theories.
- Considering particles as linear segments
that oscillate, vibrate or rotate. The wavefunction is
then related to the periodic behavior of the particle.
Among them there is Superstring theory, but also the Rotating Vector Model (RVM)
for fundamental particles.
The particularity of the RVM theory is that
inertia proceeds from pure mechanical considerations on massless
particles, whereas other theories have to presuppose that some
particles are inertial and some may be massless. The RVM theory
describes a fundamental particle as a straight-line segment of
constant length that rotates. This rotation transmits a
probability wavefunction to the particle.
To illustrate that particularity, let AB and CD
be two segment-like particles of length L that collide. For
simplicity, it is sufficient to consider the special case that:
- the rotational speed of CD is zero,
- AB is rotating in a plane perpendicular to
CD, with a rotational speed w,
- the collision point is the center of each
segment,
- the translational velocity V of CD
with respect to AB is perpendicular to AB at the instant
of collision.
As the particles are massless, they depart from
each other at a fixed constant velocity c. The velocity due to
the rotation at the extremities of AB is wL/2 .
For rotational speeds w < p c/L, the interaction is
instantaneous, both particles just touch and go.
Figure 1 shows the collision sequence in the
special case that the velocity at the extremity of AB is equal to
pc/2, i.e.
w = p c/L. The two
particles first touch and depart from each other but recollide as
the B-extremity of AB reaches the intersection of the circle and
the path of CD. This affects the final direction of the departing
velocity.
For w > p c/L, the second collision contact, located somewhere
between the center of AB and the extremity B, is non
instantaneous, as that point rotates faster than c about the
geometrical center of AB: AB pushes CD. The two particles glide
on each other for a little while. During this interaction, the
contact point progresses in the direction of one of the
extremities. As soon as the contact point has reached that
extremity, both particles depart from each other at the velocity
c. This non-instantaneity of the interaction may be interpreted
as inertia, especially when the extremely rapidly rotating
segment, an electron say, has to plough its way through a swarm
of slowly rotating particles, photons or neutrinos say. In that
case, the electron is constantly hindered in its progress through
space. The electron is also constantly projecting encountered
photons: it sets up an electromagnetic field varying with its
acceleration or deceleration.
In the given interpretation, it appears that
the measure of inertia depends on w. The measure of inertia may
be assimilated to mass and the rotational speed w of the particle
may be assimilated to internal energy. The greater the internal
energy, the greater the mass. Further investigation is needed to
verify if this dependence is of the form E = mc˛.
| Figure 1: Collision
sequance between AB and CD seen in the reference
framework of AB, with w = p c/L. |
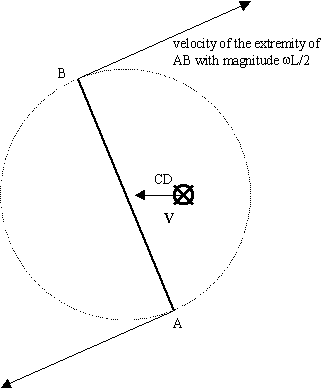 |
| Figure 1a: First step. Vector
particles AB and CD before collision. |
 |
| Figure 1b: Second step. Vector
particles AB and CD at the instant of collision. |
 |
| Figure 1c: Third step. Vector
particles AB and CD just after the instant of collision. |
 |
| Figure 1d: Fourth step. Vector
particles AB and CD at the instant of recollision. |
References
Dijksman A., 1999. Fusion 75 (in french),
translated at http://materion.free.fr/physique/reconsider.htm.




